连续

设函数y=f(x)在点x0处连续,则y=f(x)在x0处的极限存在。
如果x0是函数f(x)的间断点,且左极限及右极限都存在,则称x0为函数f(x)的第一类间断点
第一类间断点[可去间断点 + 跳跃间断点]
左右极限都存在且相等时,属于第一类间断点,且为可去间断点
左右极限都存在但不相等时,属于第一类间断点,且为跳跃间断点
左右极限至少有一个不存在时,属于第二类间断点
求初等函数的间断点即求不在函数定义域内的点,而使两个分母分别为0的点不在定义域内
初等函数在其定义区间每点处都是连续的,所以找初等函数的间断点,只需要找出其无定义的点即可
连续函数性质的应用
证明连续的题:
1、先说明函数___在[ , ]上连续,因为…
2、f(?) > 0,f(?) < 0 根据零点定理**可知函数式在[ , ]内至少有… (如果函数y= f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0**,那么,函数y= f(x)在区间(a,b)内有零点,即至少存在一个c∈(a,b),使得f(c)=0,这个c也就是方程f(x)= 0的根)
3、至少的正根可以根据函数f() > 0, f() < 0来判定,至多的正根可以根据函数的导数大于0判断单调递增来说明。

连续性+导数(可导性)
- 法线:k * k法 = -1
- 两条直线若都存在斜率且平行,则两条直线的斜率相等
- sin2x = 2sinxcosx (sin2x)’ = 2cos2x
- cos2x = $2cosx^2$ - 1 = 1 - $2sinx^2$ (cos2x)’ = -2sin2x
- tan2x = $sec^2x$ - 1 (tan2x)’ = 2sec^2x
导数的定义
导数的定义技巧1
导数的定义技巧2
导数的定义技巧3
连续性+导数大题
- 大题部分:解决该类问题的基本思路根据分段函数在其分界点处的性质来确定所含常数的值,若一函数在其分界点可导,首先在该点**连续;而在分界点的导数则按导数定义或左右导数**的定义来导
- ①先根据f(?) 带入两个式子 若 f1(?) = f2(?) 则证明该分段函数在x=?处是否连续;②之后根据f’-(?) 与 f’+(?)是否相等来判断该分段函数是否可导
- 函数y = f(x) 在点x0处左可导、右可导,并且左右导数相等,y = f(x)在点x0处才可导;函数y = f(x)在点x0处可导,必在此点连续;函数y=f(x) 在点x0处连续,未必在此点可导
导数+隐函数
$x^x$=$e^xlnx$
对于函数y=u(x)$^v$$^x$,其中u(x) > 0求导,可采用公式变形法,变形成复合指数函数,y=e^[v(x)lnu(x)]
y=f(x+1),y’=f’(x+1) + (x+1)’
- 可导的奇函数的导数为偶函数,可导的偶函数的导数为奇函数
- 隐函数求导方法:求y对x的导数时要用符合函数的求导法则,然后将含有y’的项放到等式的一端,不含y’的项移到另一端,求y‘。【只要见到隐函数里的y’就把它再求导一遍 (+2xy)’ = 2y+2xy’、 (y^2) = 2y’y】
- 如对数函数f(x)=u(x)^v(x) 求导可用**对数求导法 **[两边取自然对数]
- 如指数函数y=e^v(x)lnu(x) 公式变形法[变形成复合]
- 欲求由方程F(x,y)=0所确定的隐函数y=f(x)的导数,要把方程中的x看作自变量,而将y视为x的函数,方程中关于y的函数便是x的复合函数,用复合函数的求导方法,即可得到关于y’的一次方程,从中解得y’即为所求
高阶导数
- 求高阶导数的方法有不完全归纳法,即求出所给函数的1-3阶或4阶导数后,分析所得结果的规律,写出n阶导数↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
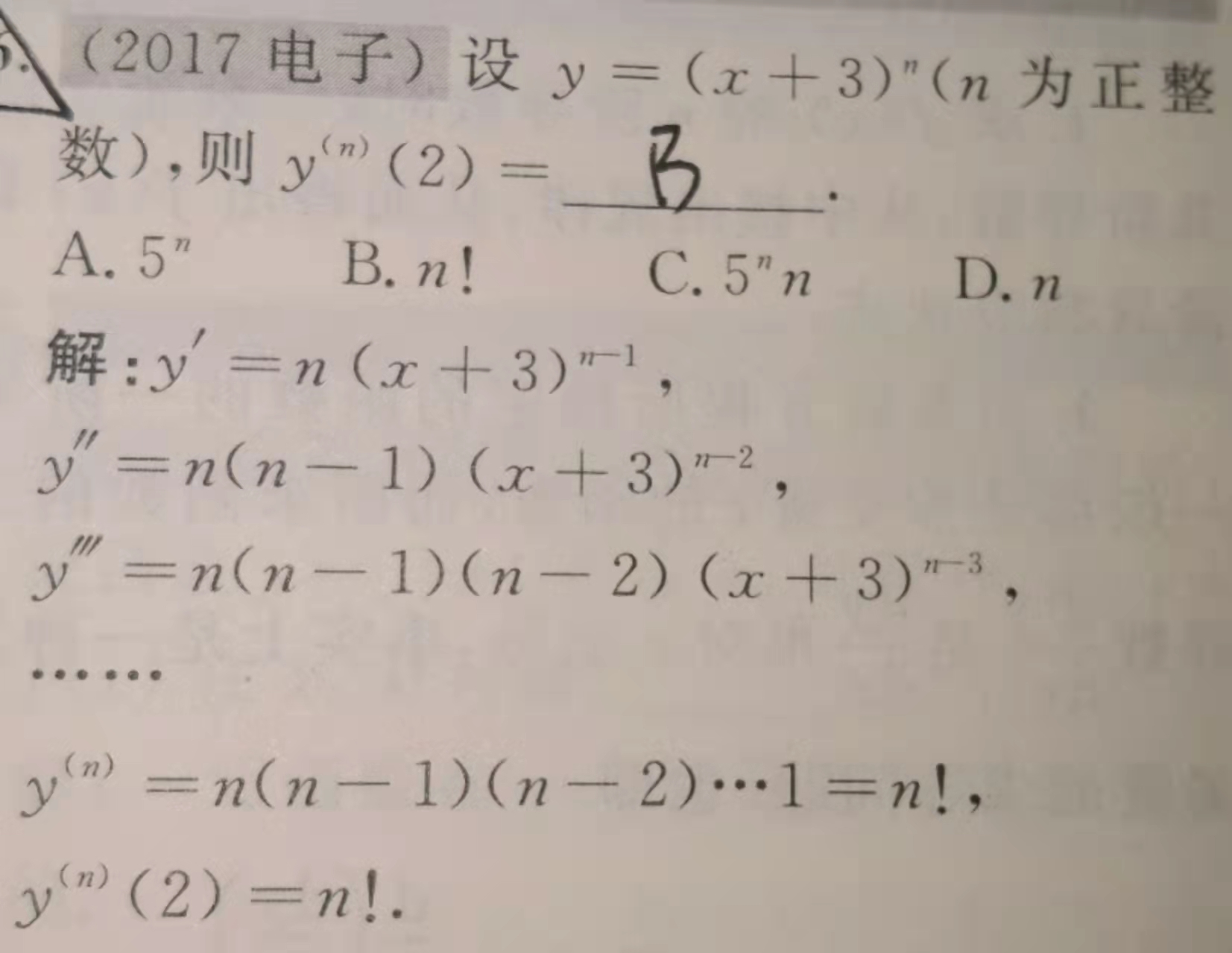

- (x^3^)^(5)^表示x^3^的五阶导数,根据幂函数求导公式易得:第三阶导数为常数,因此第四阶和第五阶导数必为0
f(x) = x^n^ 的n+1阶导数为0 => f(x) = (x^n^)^(n+1)^ = 0
- (d^2^y)/(dx^2^) 高级模板↓

高级二次求导含复合变量

